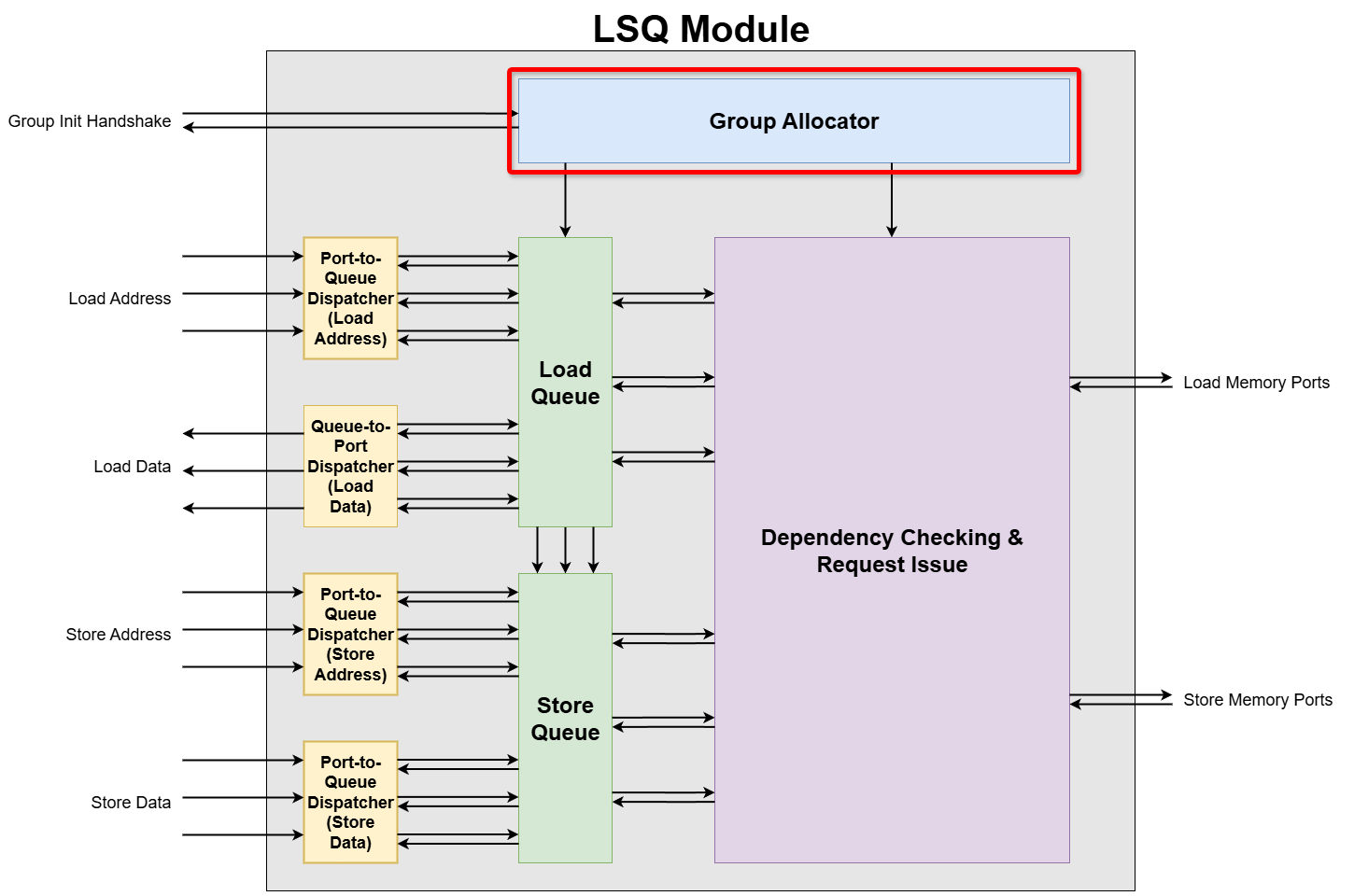
Group Allocator
This document explains how groups are allocated to the Load-Store Queue (LSQ) in a dataflow circuit.
1. Overview and Purpose
Dataflow circuits have no inherent notion of sequential instructions, and therefore no Fetch or Decode stages. This is a critical problem, because a traditional LSQ relies on this intrinsic program order to resolve potential memory dependencies. Without it, the LSQ is blind.
The solution to this problem is a concept called group allocation. A group is defined as a sequence of memory accesses that are known to execute together, without interruption from control flow. By allocating this entire group into the LSQ at once, we provide the LSQ with the necessary ordering information that was missing.
The Group Allocator is a module that manages entry allocation for the Load-Store Queue (LSQ).
2. Group Allocator Internal Blocks
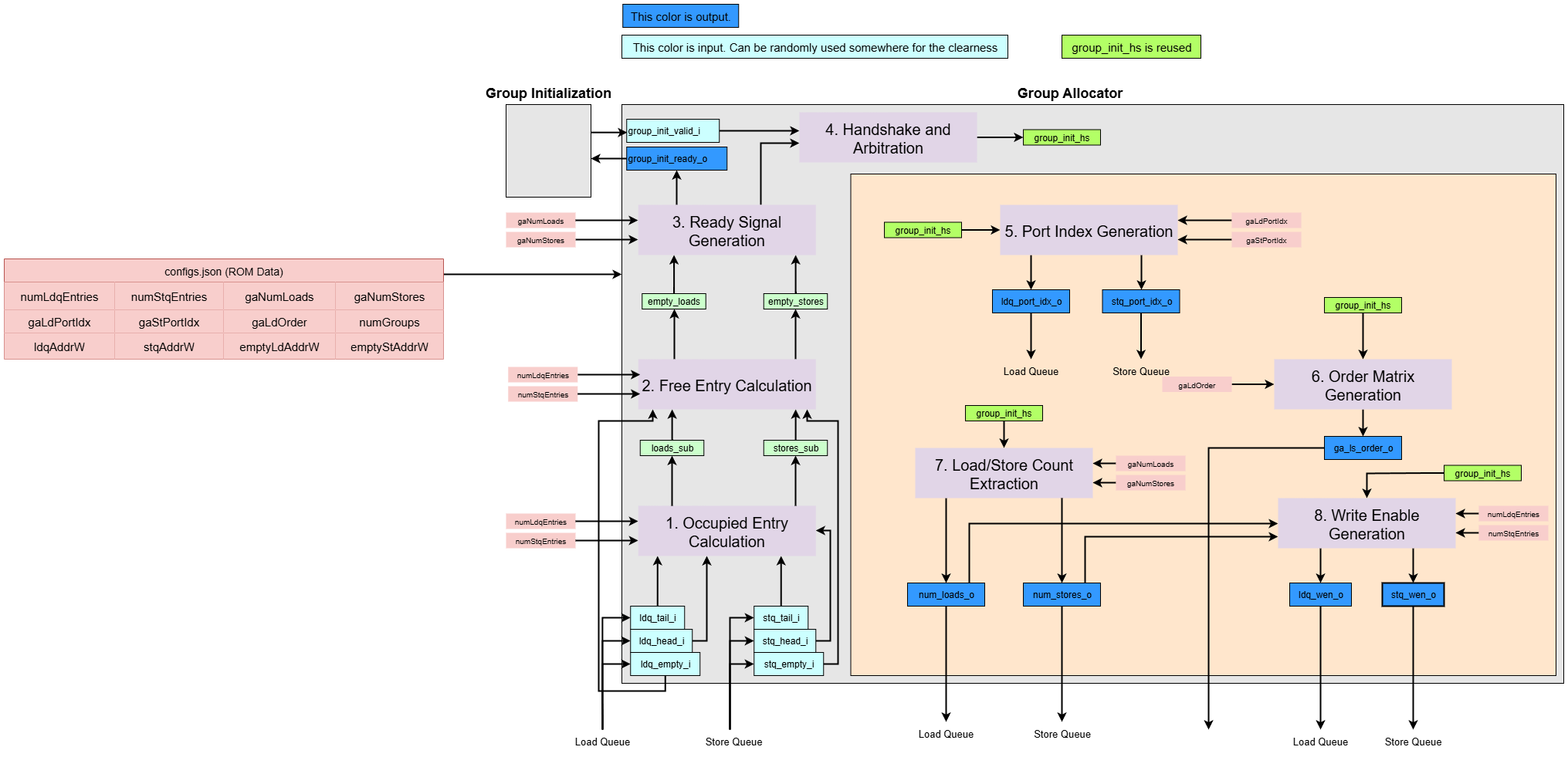
Let’s assume the following generic parameters for dimensionality:
N_GROUPS: The total number of groups.N_LDQ_ENTRIES: The total number of entries in the Load Queue.N_STQ_ENTRIES: The total number of entries in the Store Queue.LDQ_ADDR_WIDTH: The bit-width required to index an entry in the Load Queue (i.e.,ceil(log2(N_LDQ_ENTRIES))).STQ_ADDR_WIDTH: The bit-width required to index an entry in the Store Queue (i.e.,ceil(log2(N_STQ_ENTRIES))).LDP_ADDR_WIDTH: The bit-width required to index the port for a load.STP_ADDR_WIDTH: The bit-width required to index the port for a store.
Signal Naming and Dimensionality:
This module is generated from a higher-level description (e.g., in Python), which results in a specific convention for signal naming in the final VHDL code. It’s important to understand this convention when interpreting diagrams and signal tables.
-
Generation Pattern: A signal that is conceptually an array in the source code (e.g.,
group_init_valid_i) is “unrolled” into multiple, distinct signals in the VHDL entity. The generated VHDL signals are indexed with a suffix, such asgroup_init_valid_{g}_i, where{g}is the group index. -
Interpreting Diagrams: If a diagram or conceptual description uses a base name without an index (e.g.,
group_init_valid_i), it represents a collection of signals. The actual dimension is expanded based on the context:- Group-related signals (like
group_init_valid_i) are expanded by the number of groups (N_GROUPS). - Load queue-related signals (like
ldq_wen_o) are expanded by the number of load queue entries (N_LDQ_ENTRIES). - Store queue-related signals (like
stq_wen_o) are expanded by the number of store queue entries (N_STQ_ENTRIES).
- Group-related signals (like
Interface Signals
In the VHDL Signal Name column, the following placeholders are used: {g} for the group index, {le} for the Load Queue entry index, and {se} for the Store Queue entry index.
| Python Variable Name | VHDL Signal Name | Direction | Dimensionality | Description |
|---|---|---|---|---|
| Inputs | ||||
group_init_valid_i | group_init_valid_{g}_i | Input | std_logic | Valid signal indicating a request to allocate group g. |
ldq_tail_i | ldq_tail_i | Input | std_logic_vector(LDQ_ADDR_WIDTH-1:0) | Current tail pointer of the Load Queue. |
ldq_head_i | ldq_head_i | Input | std_logic_vector(LDQ_ADDR_WIDTH-1:0) | Current head pointer of the Load Queue. |
ldq_empty_i | ldq_empty_i | Input | std_logic | A flag indicating if the Load Queue is empty. |
stq_tail_i | stq_tail_i | Input | std_logic_vector(STQ_ADDR_WIDTH-1:0) | Current tail pointer of the Store Queue. |
stq_head_i | stq_head_i | Input | std_logic_vector(STQ_ADDR_WIDTH-1:0) | Current head pointer of the Store Queue. |
stq_empty_i | stq_empty_i | Input | std_logic | A flag indicating if the Store Queue is empty. |
| Outputs | ||||
group_init_ready_o | group_init_ready_{g}_o | Output | std_logic | Ready signal indicating the allocator can accept a request for group g. |
ldq_wen_o | ldq_wen_{le}_o | Output | std_logic | Write enable signal for Load Queue entry {le}. |
num_loads_o | num_loads_o | Output | std_logic_vector(LDQ_ADDR_WIDTH-1:0) | The number of loads in the newly allocated group. |
ldq_port_idx_o | ldq_port_idx_{le}_o | Output | std_logic_vector(LDP_ADDR_WIDTH-1:0) | The source port index for the operation to be written into Load Queue entry {le}. |
stq_wen_o | stq_wen_{se}_o | Output | std_logic | Write enable signal for Store Queue entry {se}. |
num_stores_o | num_stores_o | Output | std_logic_vector(STQ_ADDR_WIDTH-1:0) | The number of stores in the newly allocated group. |
stq_port_idx_o | stq_port_idx_{se}_o | Output | std_logic_vector(STP_ADDR_WIDTH-1:0) | The source port index for the operation to be written into Store Queue entry {se}. |
ga_ls_order_o | ga_ls_order_{le}_o | Output | std_logic_vector(N_STQ_ENTRIES-1:0) | For the load in a load queue entry {le}, this vector indicates its order dependency relative to all store queue entries. |
The Group Allocator has the following responsibilities:
-
Preliminary Free Entry Calculator
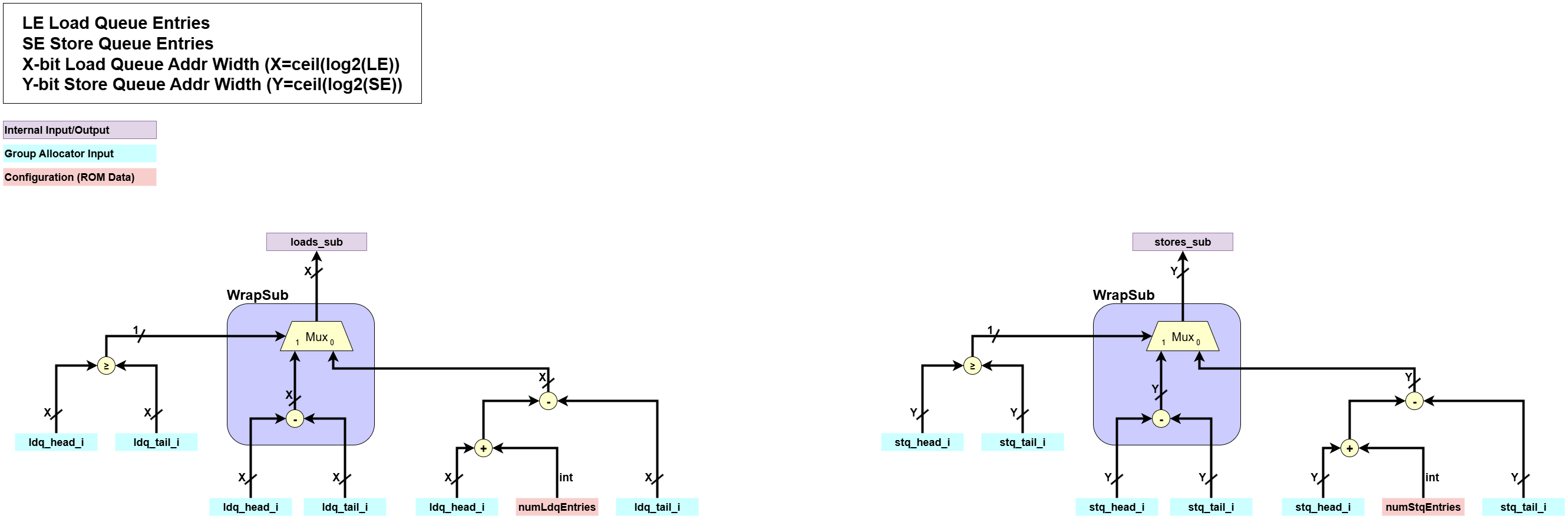
This block performs an initial calculation of the number of free entries in each queue.- Input:
ldq_head_i,ldq_tail_i: Head and tail pointers for the Load Queue.stq_head_i,stq_tail_i: Head and tail pointers for the Store Queue.
- Processing:
- It performs a cyclic subtraction (
WrapSub) of the pointers for each queue. This calculation gives the number of empty slots but is ambiguous when the two pointers are the same (head == tail) since it can either mean empty or full.if head >= tail: out = head - tail else: out = (head + numEntries) - tail
- It performs a cyclic subtraction (
- Output:
loads_sub,stores_sub: Intermediate signals holding the result of the cyclic subtraction for each queue.
- Input:
-
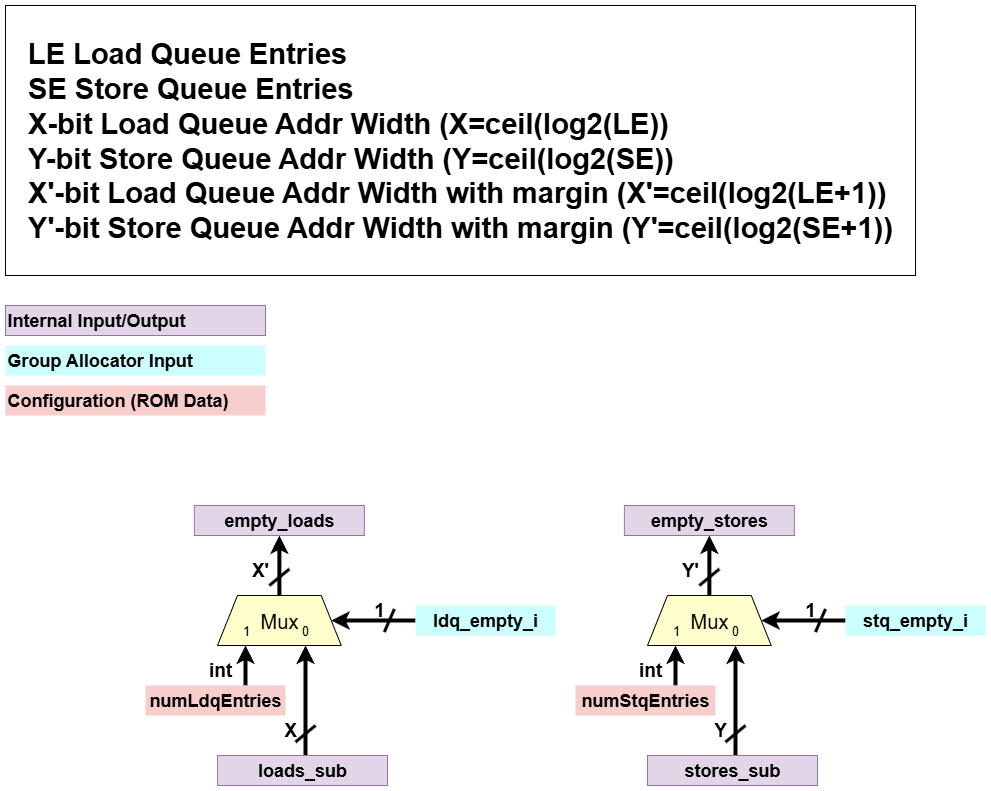
Free Entry Calculation
This block determines the final number of free entries available in each queue.- Input:
loads_sub,stores_sub: The tentative free entry counts from the previous block.ldq_empty_i,stq_empty_i: Flags indicating if each queue is empty.
- Processing:
- It uses multiplexer logic to resolve the ambiguity of the previous step.
- If a queue’s
emptyflag is asserted, it outputs the maximum queue size (numLdqEntriesornumStqEntries). - Otherwise, it outputs the result from the
WrapSubcalculation.
- Output:
empty_loads,empty_stores: The definitive number of free entries in the load and store queues.
- Input:
-
Ready Signal Generation
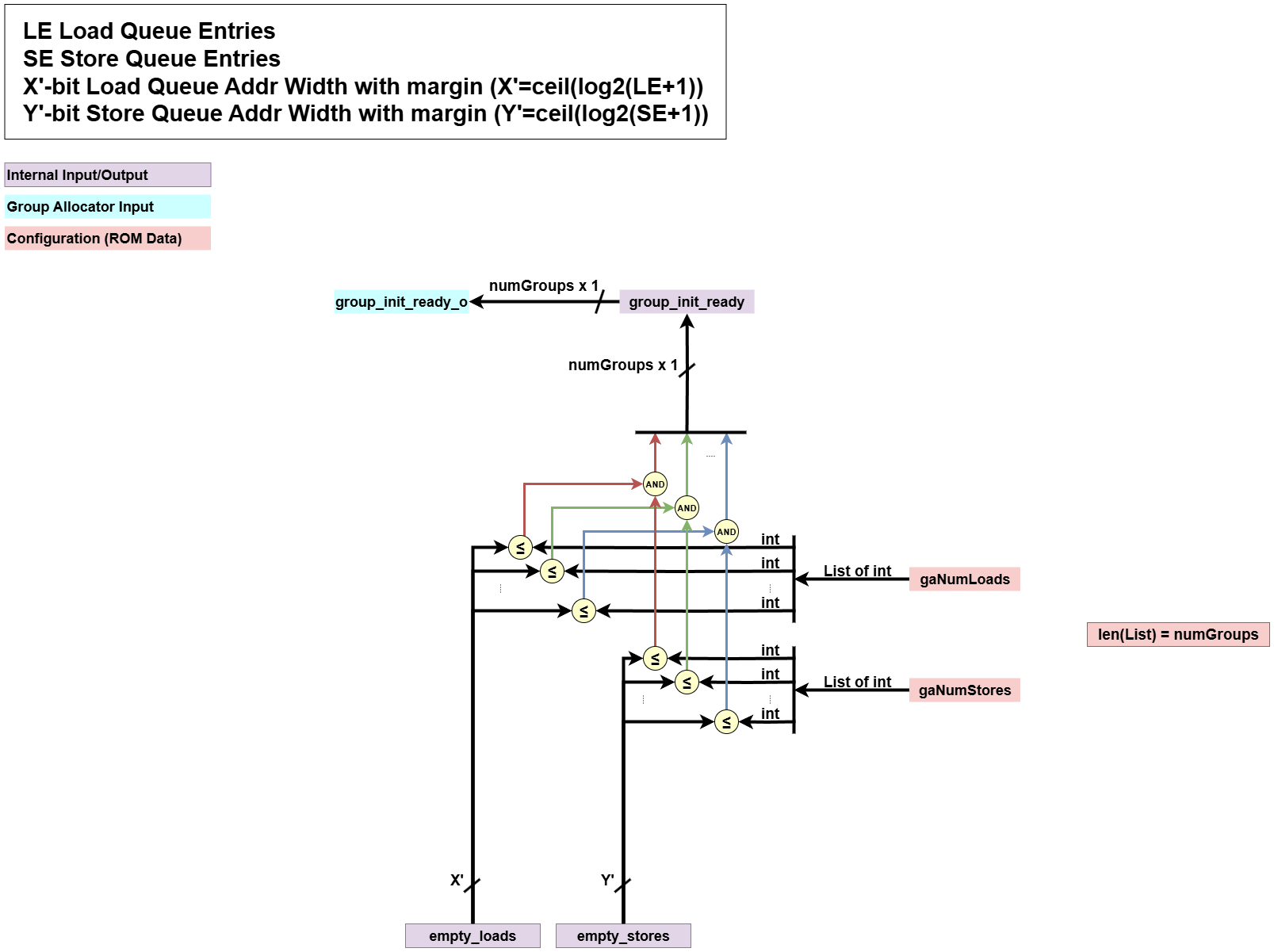
This block checks if there is sufficient space in the queues for each potential group.- Input:
empty_loads,empty_stores: The number of free entries available in each queue.gaNumLoads,gaNumStores: Configuration arrays specifying the number of loads and stores required by each group.
- Processing:
- For each group, it compares the available space (
empty_loads,empty_stores) with the required space (gaNumLoads[g],gaNumStores[g]). - A group is considered “ready” only if there is enough space for both its loads and its stores.
- For each group, it compares the available space (
- Output:
group_init_ready: An array of ready signals, one for each group, indicating whether it could be allocated.group_init_ready_o: The final ready signals sent to the external logic.
- Input:
-
Handshake and Arbitration
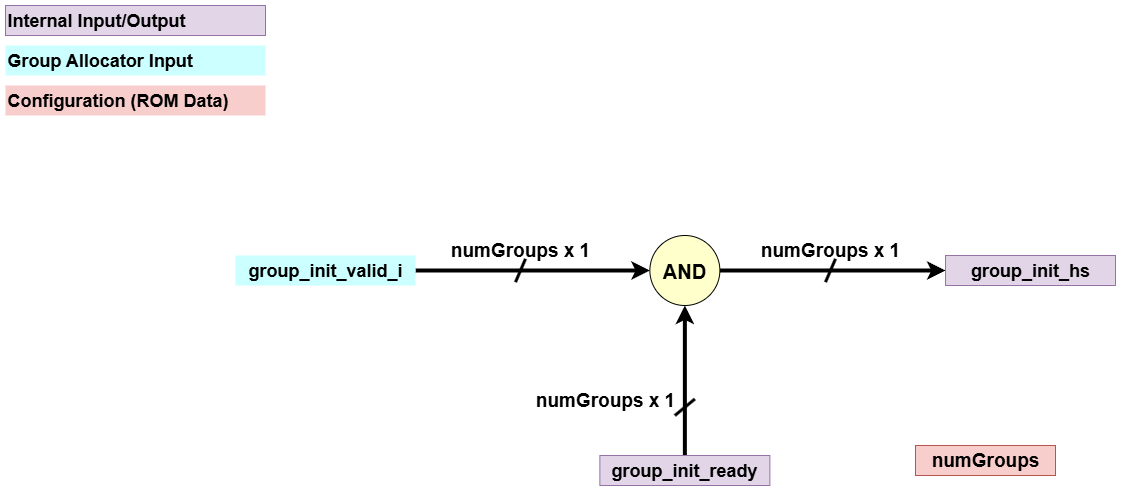
This block performs the final handshake to select a single allocated group for the current cycle. However, the arbitration happens when one of the configuration signalgaMultiis on, and this diagram depicts whengaMultiis off.- Input:
group_init_ready: The readiness status for each group from the previous block.group_init_valid_i: The external valid signals for each group.- (Optional)
ga_rr_mask: A round-robin mask used for arbitration if multiple groups can be allocated (gaMultiis true).
- Processing:
- It combines the
readyandvalidsignals. A group must be both ready and valid to be a candidate for allocation. - If multiple groups are candidates, an arbitrator (e.g.,
CyclicPriorityMasking) selects a single group. IfgaMultiis false, it assumes only one valid allocation request can occur at a time as depicted.
- It combines the
- Output:
group_init_hs: A one-hot signal indicating the single group that will be allocated at the current cycle.
- Input:
-
Port Index Generation
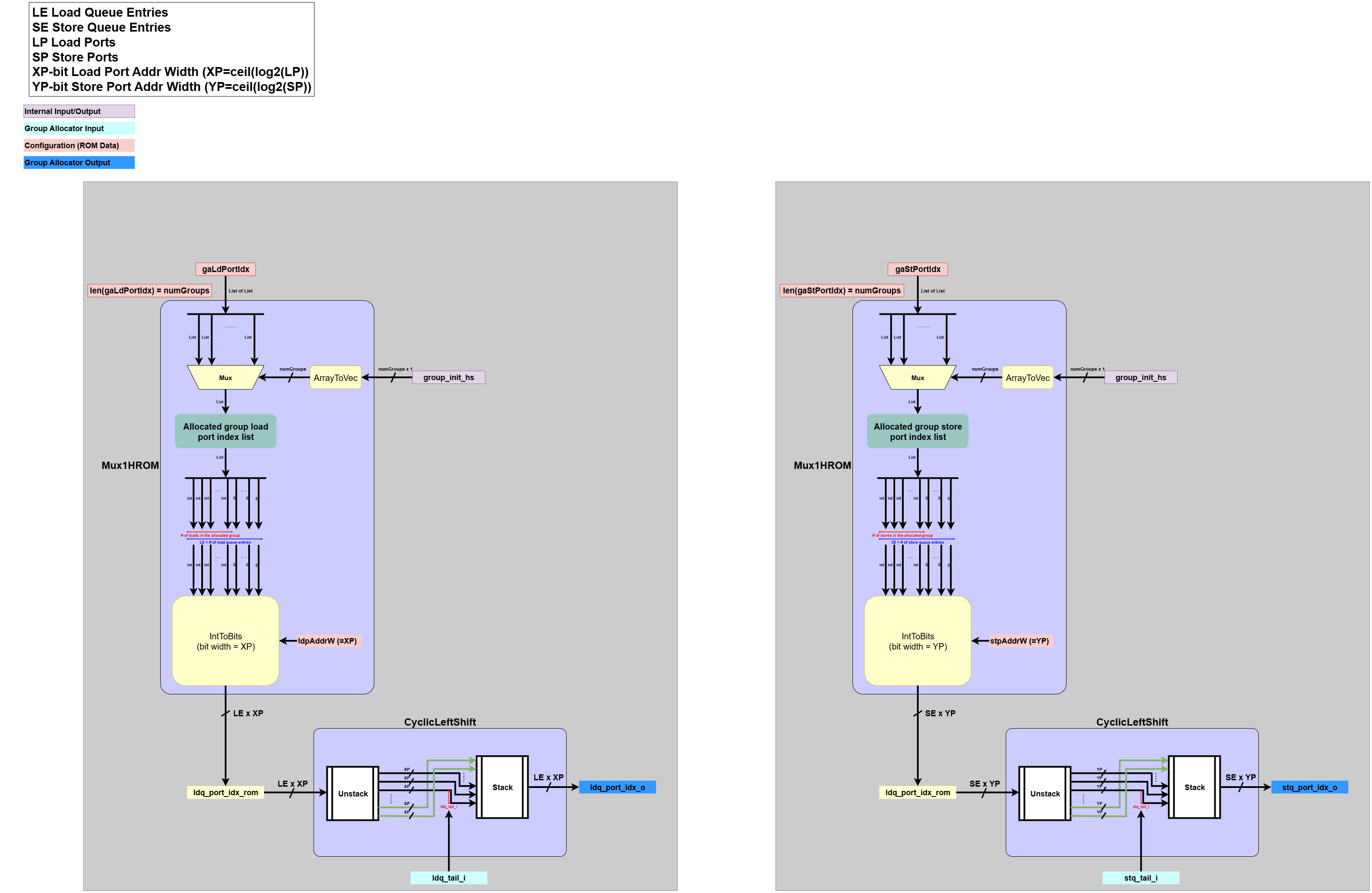
This block generates the correctly aligned port indices for the entries being allocated.- Input:
group_init_hs: A one-hot signal indicating the single group that will be allocated at the current cycle.ldq_tail_i,stq_tail_i: The current tail pointers of the queues.gaLdPortIdx,gaStPortIdx: Pre-compiled ROMs containing the port indices for each group.
- Processing:
- Uses the
group_init_hssignal to perform a ROM lookup (Mux1HROM), selecting the list of port indices for the allocated group. - Performs
CyclicLeftShifton the selected list, using the corresponding queue’stailpointer as the shift amount. This aligns the indices to the correct physical queue entry slots.
- Uses the
- Output:
ldq_port_idx_o,stq_port_idx_o: The final, shifted port indices to be written into the newly allocated queue entries.
- Input:
-
Order Matrix Generation
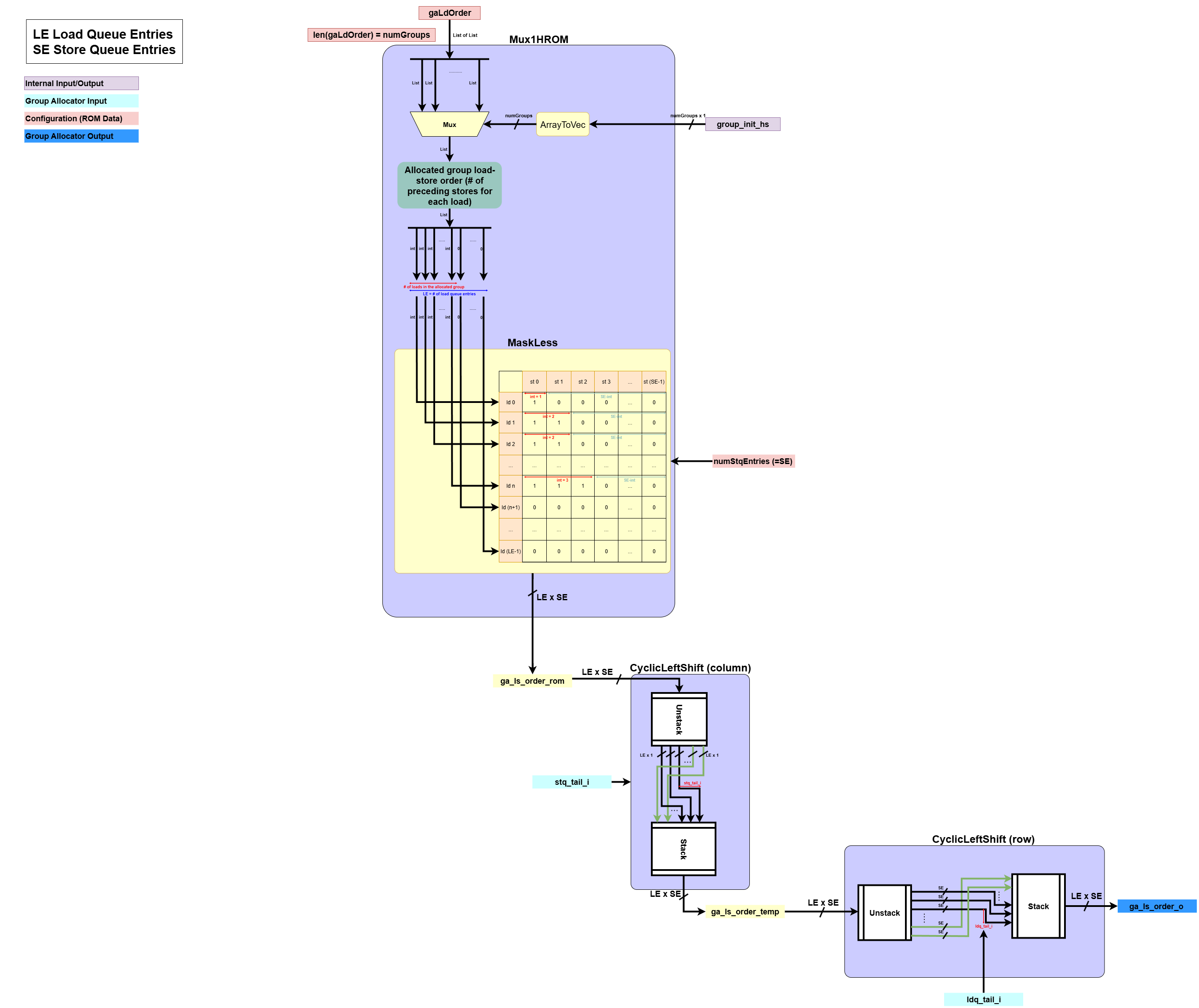
This block generates the load-store order matrix between the new loads and stores in the allocated group.- Input:
group_init_hs: A one-hot signal indicating the single group that will be allocated at the current cycle.ldq_tail_i,stq_tail_i: The current tail pointers of the queues.gaLdOrder: A pre-compiled ROM containing the load-store order information for each group. For each group, the corresponding list indicates, from the perspective of a load, the number of stores that come before it within the same group.
- Processing:
- Uses
group_init_hsto perform a ROM lookup, selecting the order information for the allocated group. This information is used to build an un-aligned load-store order matrix. - A
1in(le, se)indicates thatstore_{se}comes beforeload_{le}. This is built by the functionMaskLess. - Performs
CyclicLeftShifton this matrix two times, shifting it horizontally bystq_tail_iand vertically byldq_tail_i. This correctly places the sub-matrix within the LSQ’s main order matrix.
- Uses
- Output:
ga_ls_order_o: The final, shifted load-store order matrix defining the order of the new loads and stores.
- Input:
-
Load/Store Count Extraction
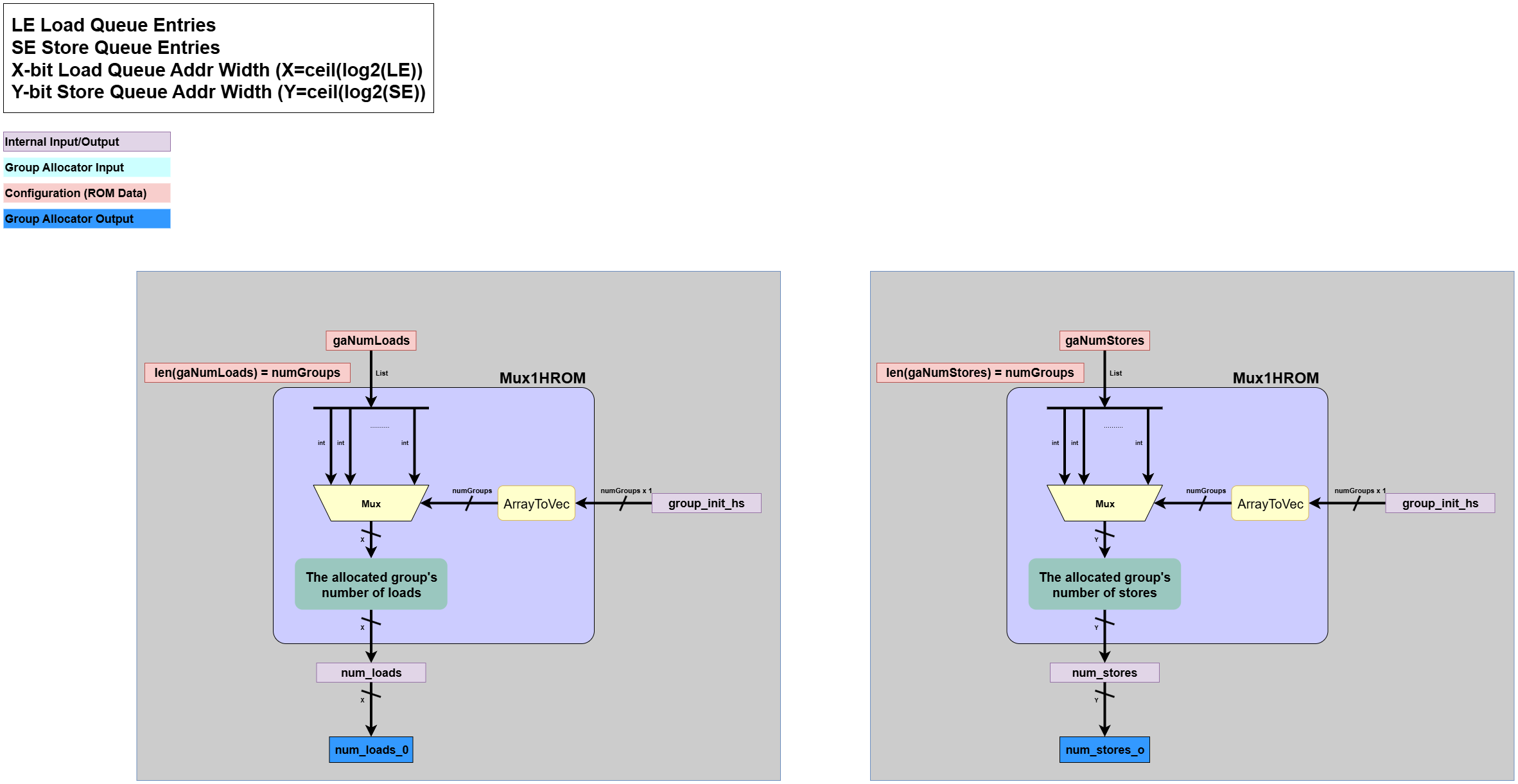
This block extracts the number of loads and stores for the allocated group.- Input:
group_init_hs: A one-hot signal indicating the single group that will be allocated at the current cycle.gaNumLoads,gaNumStores: Pre-compiled ROMs containing the load/store counts for each group.
- Processing:
- Performs a simple ROM lookup (
Mux1HROM) usinggroup_init_hsto select the number of loads and stores corresponding to the allocated group.
- Performs a simple ROM lookup (
- Output:
num_loads_o,num_stores_o: The number of loads and stores in the newly allocated group.
- Input:
-
Write Enable Generation
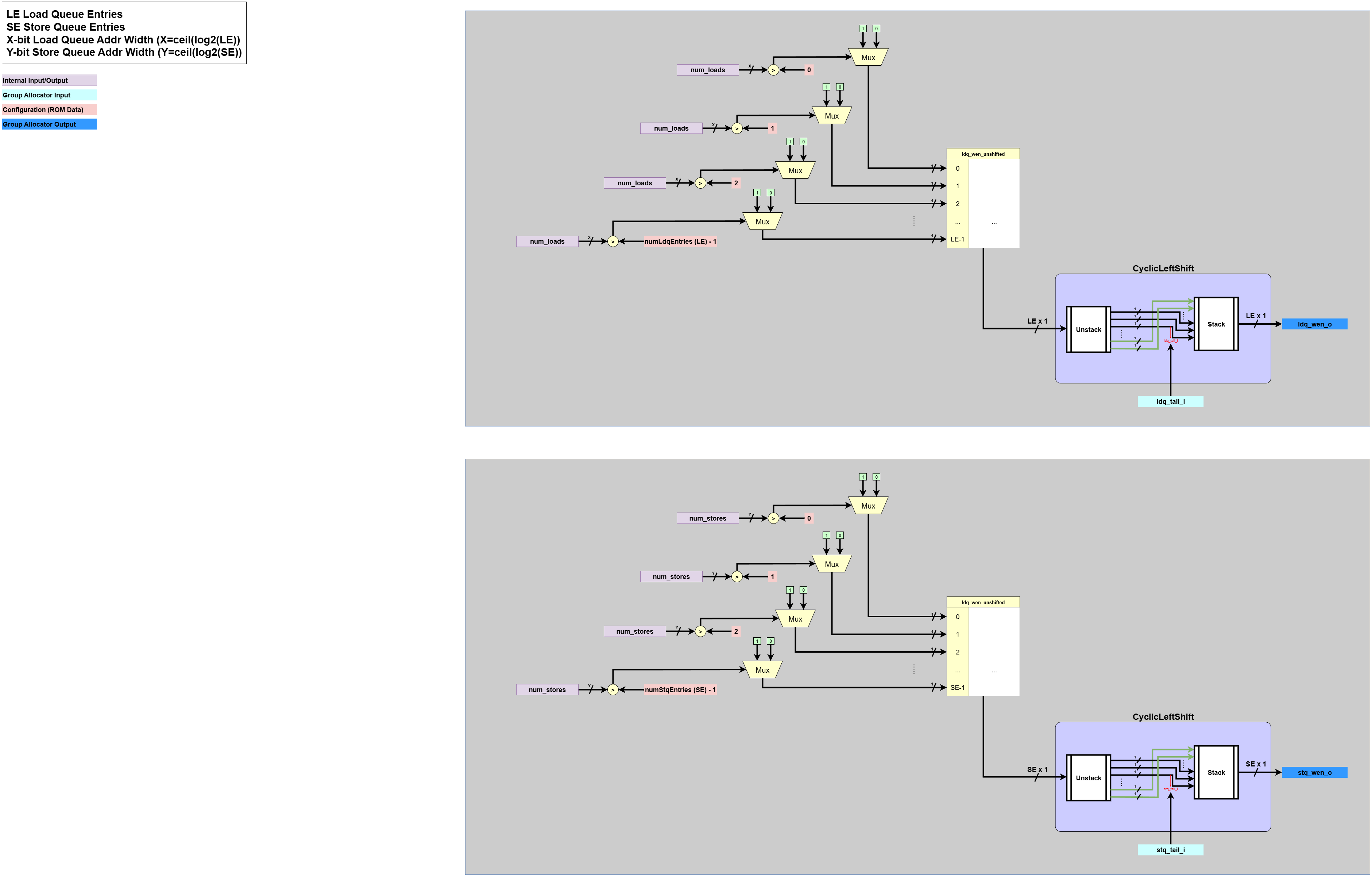
This final block generates the write-enable signals to allocate the new queue entries.- Input:
num_loads,num_stores: The load/store counts from the previous block.ldq_tail_i,stq_tail_i: The current tail pointers of the queues.
- Processing:
- First, it creates an unshifted bitmask. For example, if
num_loadsis 3, the mask is...00111. - It then applies
CyclicLeftShiftto this mask, using the queue’stailpointer as the shift amount. This rotates the block of1s to start at thetailposition.
- First, it creates an unshifted bitmask. For example, if
- Output:
ldq_wen_o,stq_wen_o: The final write-enable vectors, which assert a ‘1’ for the precise entries in each queue that are being allocated.
- Input:
3. Dataflow Walkthrough
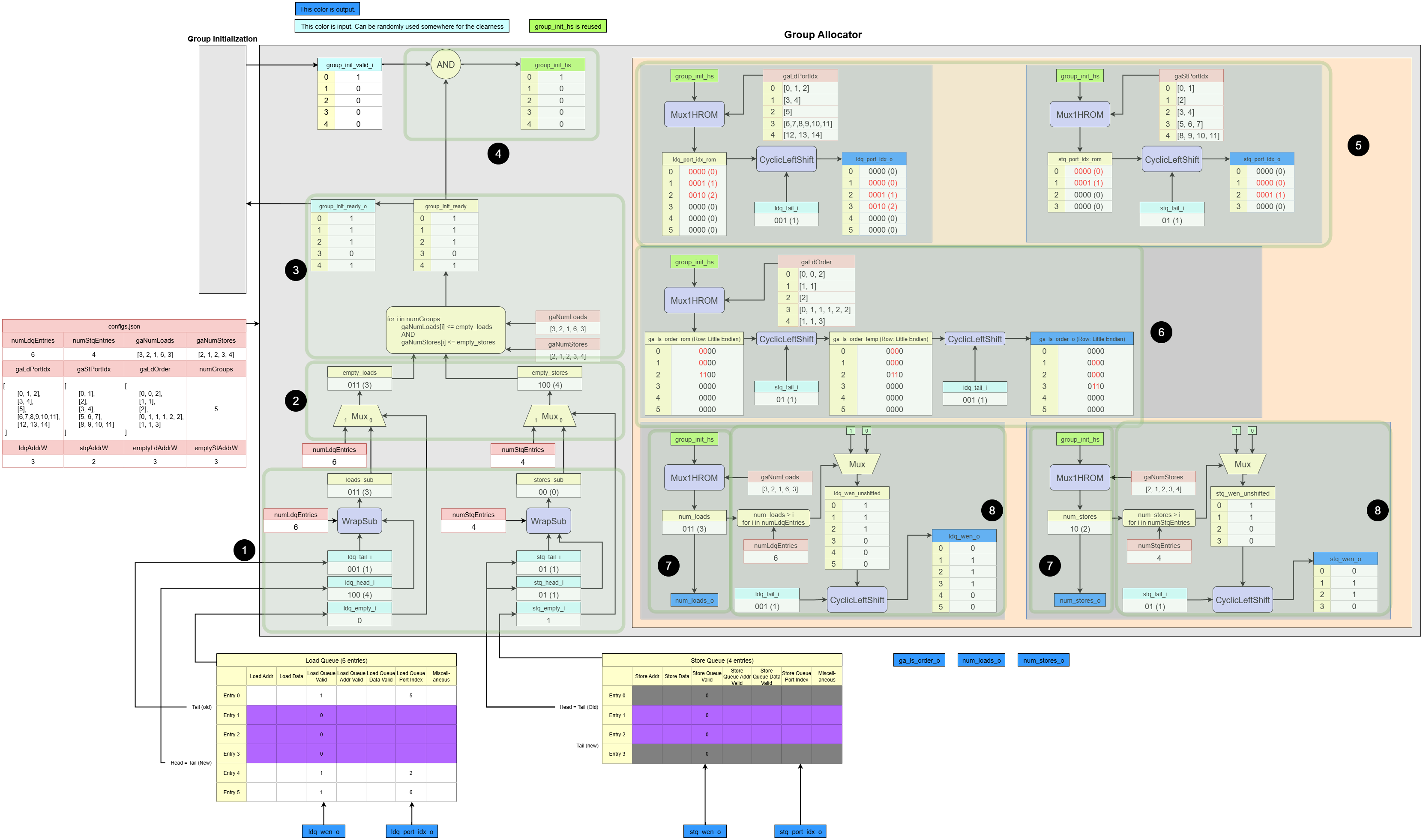
Example of Group Allocator
This walkthrough explains the step-by-step operation of the Group Allocator based on the following precise initial state:
- Queue State:
- Load Queue:
ldq_tail=1,ldq_head=4,ldq_empty_i=0 (Not Empty) - Store Queue:
stq_tail=1,stq_head=1,stq_empty_i=1 (Empty)
- Load Queue:
- Queue Sizes:
numLdqEntries=6,numStqEntries=4 - Group Allocation Request:
group_init_valid_i=[1,0,0,0,0](Only Group 0 is requesting the allocation) - Group Configurations:
gaNumLoads=[3, 2, 1, 6, 3]gaNumStores=[2, 1, 2, 3, 4]
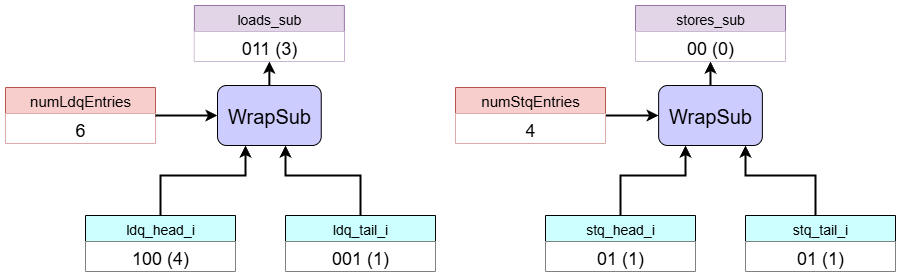
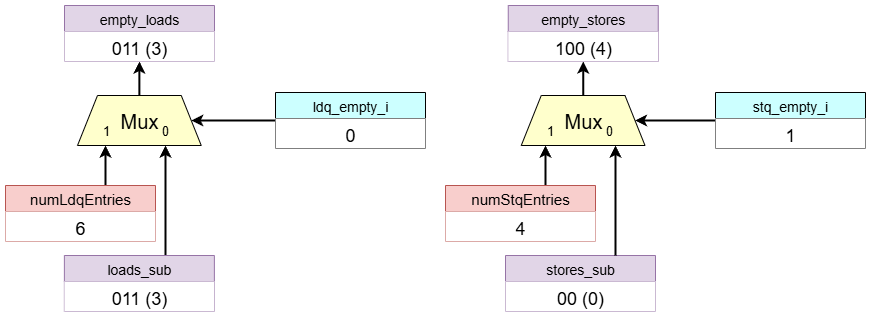
1. Preliminary Free Entry Calculation

This block calculates the tentative number of currently free entries in each queue.
- Load Queue: It performs a cyclic subtraction
ldq_head(4) -ldq_tail(1) =3. There are 3 free entries. - Store Queue: It performs a cyclic subtraction
stq_head(1) -stq_tail(1) =0. However, there are actually4free entries instead of0. This result is ambiguous and will be resolved in the next step.
2. Free Entry Calculation

This block calculates the number of available empty entries.
- Load Queue: Since
ldq_empty_iis0(false), there are 3 free entries in the load queue. - Store Queue: Since
stq_empty_iis1(true), it outputs the total queue size. There are 4 free entries in the Store Queue.
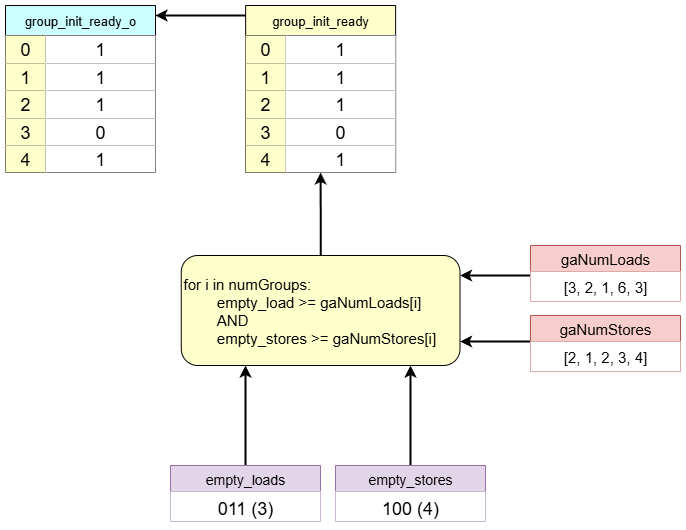
3. Ready Signal Generation

This block checks if the load queue and store queue are ready to be allocated.
- Required Space for Group 0:
gaNumLoads[0]=3,gaNumStores[0]=2.- Comparison:
- Loads: Is free space (3) >= required space (3)? Yes.
- Stores: Is free space (4) >= required space (2)? Yes.
group_init_ready[0] = 1
- Comparison:
- Required Space for Group 1:
gaNumLoads[1]=2,gaNumStores[1]=1.- Comparison:
- Loads: Is free space (3) >= required space (2)? Yes.
- Stores: Is free space (4) >= required space (1)? Yes.
group_init_ready[1] = 1
- Comparison:
- Required Space for Group 2:
gaNumLoads[2]=1,gaNumStores[2]=2.- Comparison:
- Loads: Is free space (3) >= required space (1)? Yes.
- Stores: Is free space (4) >= required space (2)? Yes.
group_init_ready[2] = 1
- Comparison:
- Required Space for Group 3:
gaNumLoads[3]=6,gaNumStores[3]=3.- Comparison:
- Loads: Is free space (3) >= required space (6)? No.
- Stores: Is free space (4) >= required space (3)? Yes.
group_init_ready[3] = 0
- Comparison:
- Required Space for Group 4:
gaNumLoads[4]=3,gaNumStores[4]=4.- Comparison:
- Loads: Is free space (3) >= required space (3)? Yes.
- Stores: Is free space (4) >= required space (4)? Yes.
group_init_ready[4] = 1
- Comparison:
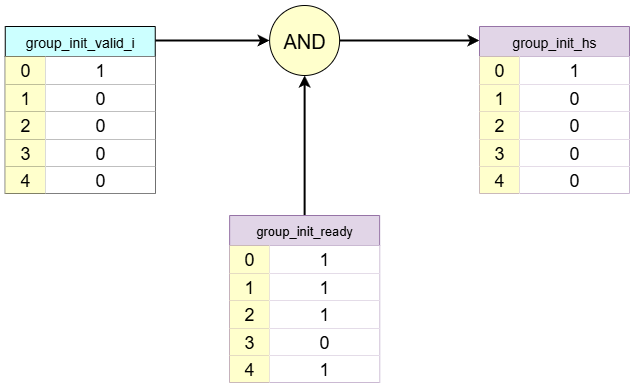
4. Handshake and Arbitration

This block performs the handshake to select an allocated group.
- The incoming request
group_init_valid_iis[1,0,0,0,0]. - The
readysignal for Group 0 is1. - The AND result is
[1,0,0,0,0], and since only one request is active, Group 0 is allocated.
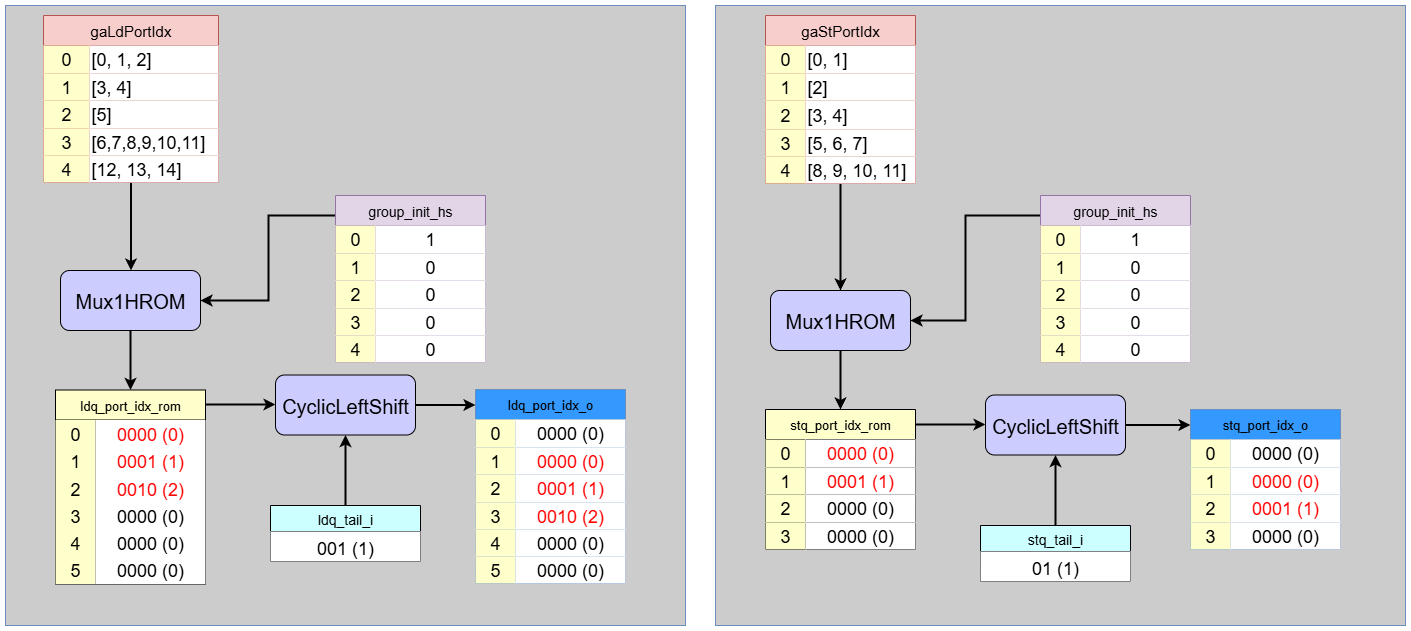
5. Port Index Generation

This block generates the correctly aligned port indices for the newly allocated entries. It first looks up the data for the allocated group (Group 0), pads it to the full queue length, and then performs the specified shift operation to align it with the tail pointer.
-
Load Port Index (
ldq_port_idx_o):- ROM Lookup: It fetches
gaLdPortIdx[0], which is[0, 1, 2]. This means thatload0_0(Group0’s 0th load),load0_1(Group0’s 1st load), andload0_2(Group0’s 2nd load) usePort 0,Port 1, andPort 2respectively. Since the load queue has 6 entries, this is padded to create the intermediate vectorldq_port_idx_rom = [0, 1, 2, 0, 0, 0]. - Alignment: These indices must be placed into the physical queue entries starting at
ldq_tail=1.- Physical
Entry 1gets Port Index0. - Physical
Entry 2gets Port Index1. - Physical
Entry 3gets Port Index2.
- Physical
- Final Vector: The resulting vector of port indices is
[0, 0, 1, 2, 0, 0]. (Note: This vector represents the indices[?, 0, 1, 2, ?, ?]aligned to the 6 queue entries, with unused entries being 0).
- ROM Lookup: It fetches
-
Store Port Index (
stq_port_idx_o):- ROM Lookup: It fetches
gaStPortIdx[0], which is[0, 1]. This is padded to the 4-entry store queue length to become[0, 1, 0, 0]. - Alignment: These are placed starting at
stq_tail=1.- Physical
Entry 1gets Port Index0. - Physical
Entry 2gets Port Index1.
- Physical
- Final Vector: The resulting vector is
[0, 0, 1, 0]. (Note: This represents[?, 0, 1, ?]aligned to the 4 queue entries).
- ROM Lookup: It fetches
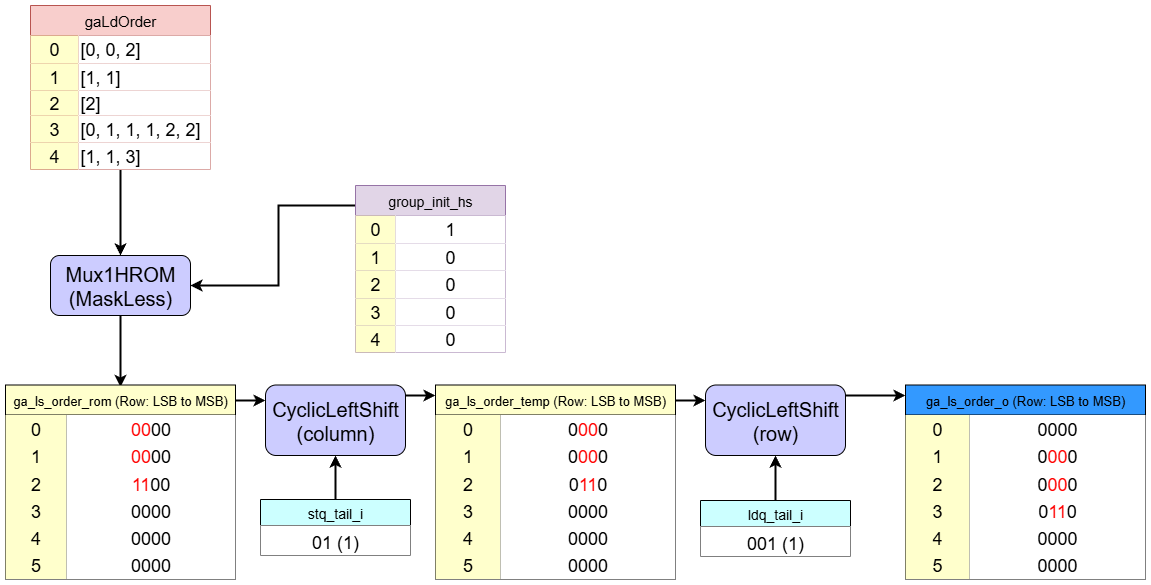
6. Order Matrix Generation

This block fetches the intra-group order matrix for Group 0 and aligns it.
-
ROM Lookup: It retrieves
gaLdOrder[0], which is[0, 0, 2]. This defines the intra-group dependencies for the group0:Load 0: There are 0 stores before it.Load 1: There are 0 stores before it.Load 2: There are 2 stores before it (Store 0andStore 1).- This creates a
3x2dependency sub-matrix:s0 s1 l0 [0, 0] l1 [0, 0] l2 [1, 1]
For this, the order matrix becomes
ga_ls_order_rom SQ0 SQ1 SQ2 SQ3 LQ Entry 0: [ 0, 0, 0, 0 ] LQ Entry 1: [ 0, 0, 0, 0 ] LQ Entry 2: [ 1, 1, 0, 0 ] LQ Entry 3: [ 0, 0, 0, 0 ] LQ Entry 4: [ 0, 0, 0, 0 ] LQ Entry 5: [ 0, 0, 0, 0 ] -
Matrix Alignment: This
3x2sub-matrix is placed into the final6x4ga_ls_order_omatrix, with its top-left corner aligned to(ldq_tail, stq_tail)which is(1, 1). The new loads occupy physical entries {1, 2, 3} and new stores occupy {1, 2}. The dependency of Load 2 (physical entry 3) on Store 0 (physical entry 1) and Store 1 (physical entry 2) is mapped accordingly. -
Final Matrix (
ga_ls_order_o): The final matrix will have1s atga_ls_order_o[3][1]andga_ls_order_o[3][2]. All other entries related to this group are0.SQ0 SQ1 SQ2 SQ3 LQ Entry 0: [ 0, 0, 0, 0 ] LQ Entry 1: [ 0, 0, 0, 0 ] // New Load 0 LQ Entry 2: [ 0, 0, 0, 0 ] // New Load 1 LQ Entry 3: [ 0, 1, 1, 0 ] // New Load 2 depends on new Store 0 & 1 LQ Entry 4: [ 0, 0, 0, 0 ] LQ Entry 5: [ 0, 0, 0, 0 ]
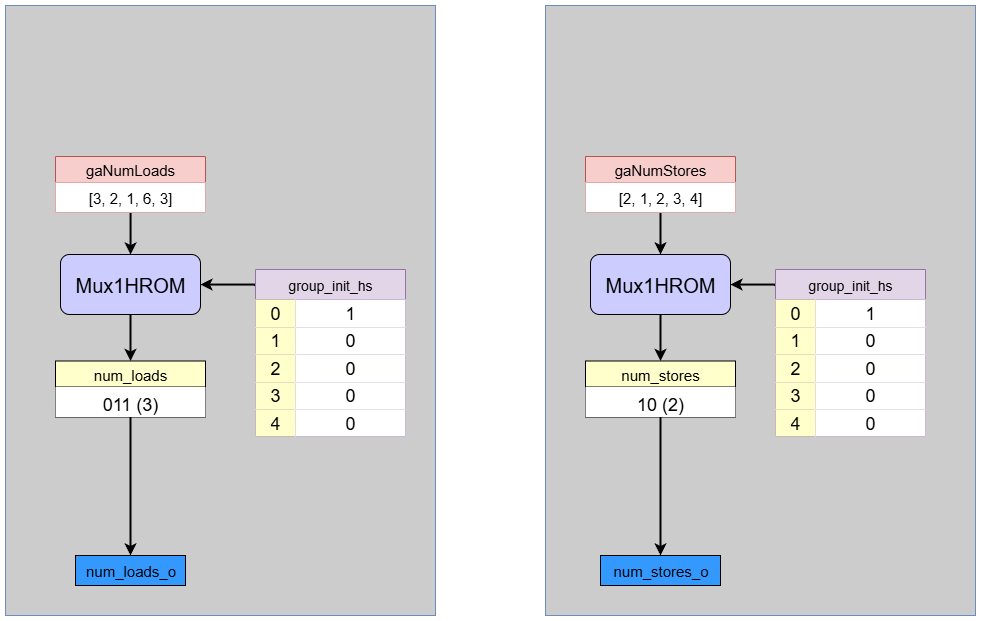
7. Load/Store Count Extraction

This block extracts the number of loads and stores for the allocated group (Group 0).
- ROM Lookup: It retrieves
gaNumLoads[0](3) andgaNumStores[0](2). - The outputs
num_loads_oandnum_stores_obecome3and2, respectively.
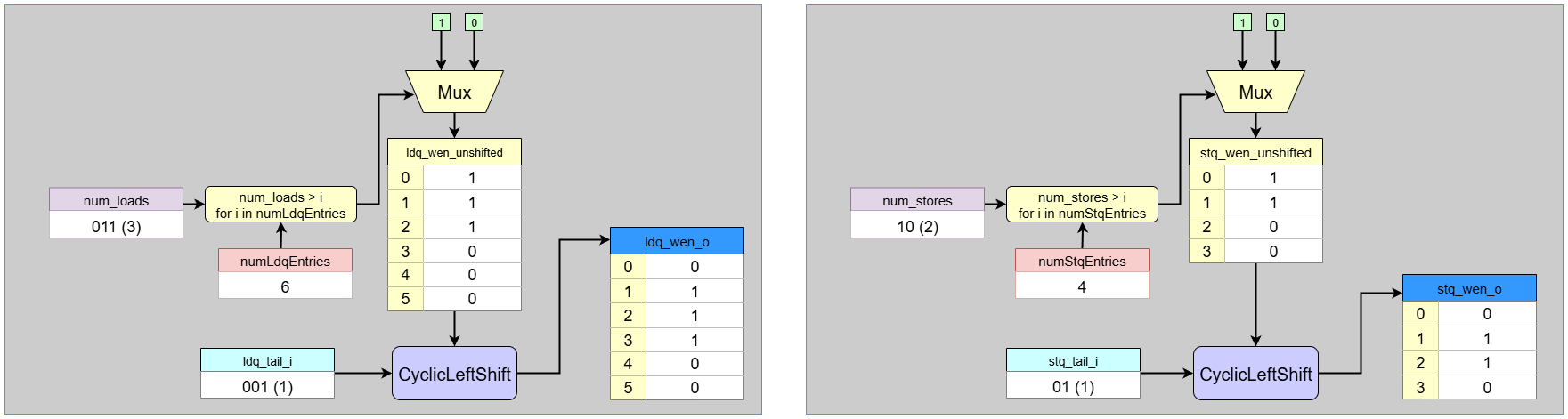
8. Write Enable Generation

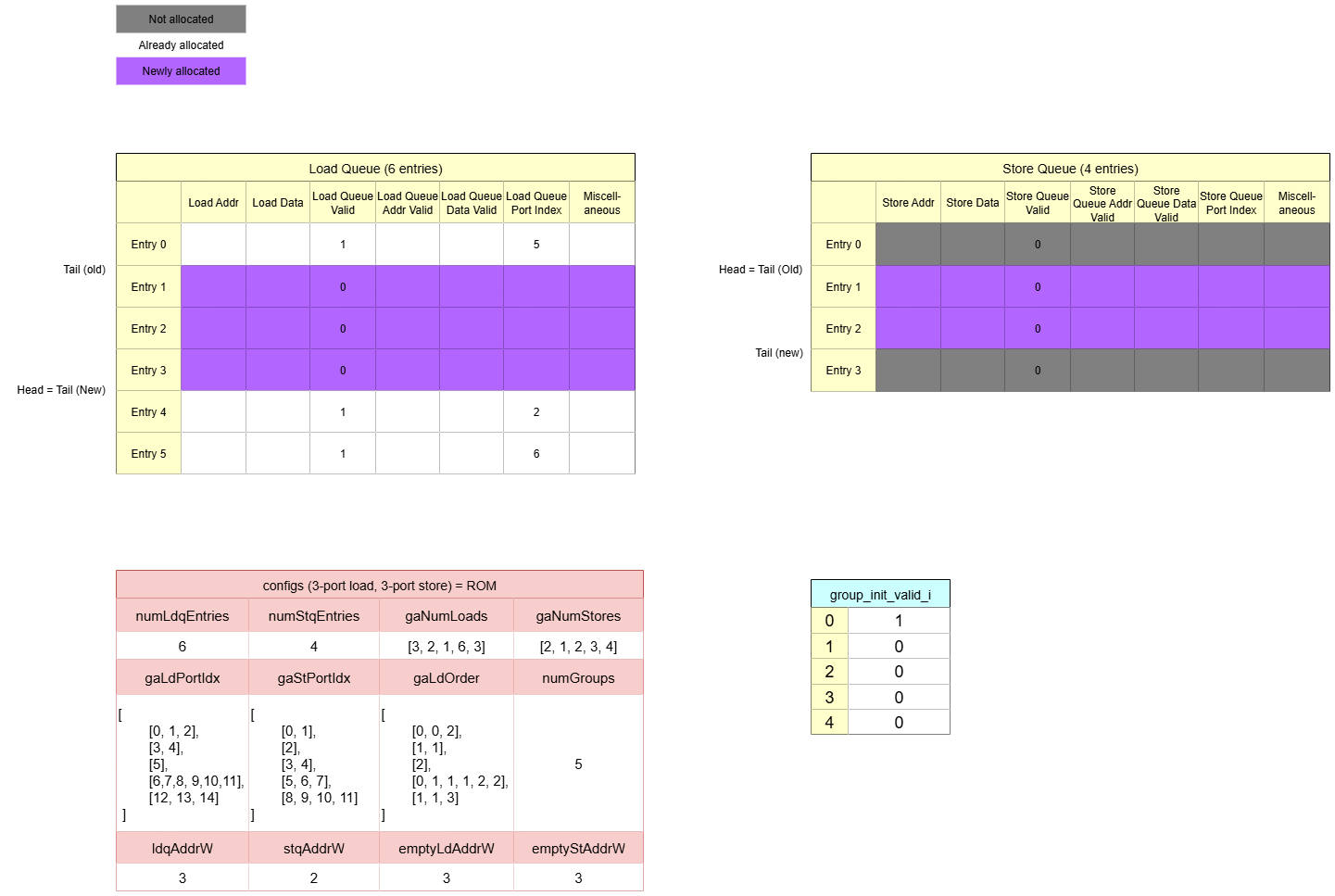
This final block generates the write-enable signals that allocate the newly allocated queue entries.
- Unshifted Mask Creation:
- Loads:
num_loads(3) creates a 6-bit unshifted mask000111. - Stores:
num_stores(2) creates a 4-bit unshifted mask0011.
- Loads:
- Cyclic Left Shift:
ldq_wen_o: The mask000111is shifted byldq_tail(1), resulting in001110.stq_wen_o: The mask0011is shifted bystq_tail(1), resulting in0110.
- These final vectors assert ‘1’ for entries 1, 2, 3 in the Load Queue and entries 1, 2 in the Store Queue, activating them for the new group.